조건:
- 1 <= n <= 2^31 - 1
의역: n개의 코인을 가지고 있고 당신은 계단식으로 코인을 쌓고자 한다.
계단식의 쌓는 방법에서 k행에는 k개의 코인으로 이루어져 있고 마지막 행(층)은 완벽하게 코인으로 채워져 있지 않을 수도 있다. ex: 코인이 7개인 경우( 1행(4층-꼭대기) -> 1개, 2행(3층) -> 2개, 3행(2층) -> 3개, 4행(1층) -> 1개)
7 = 1 + 2 + 3 + 1
결론: 정수 n이 주어질 때 이를 계단식으로 쌓았을 때 완벽하게 채워진 행의 개수를 반환해라.
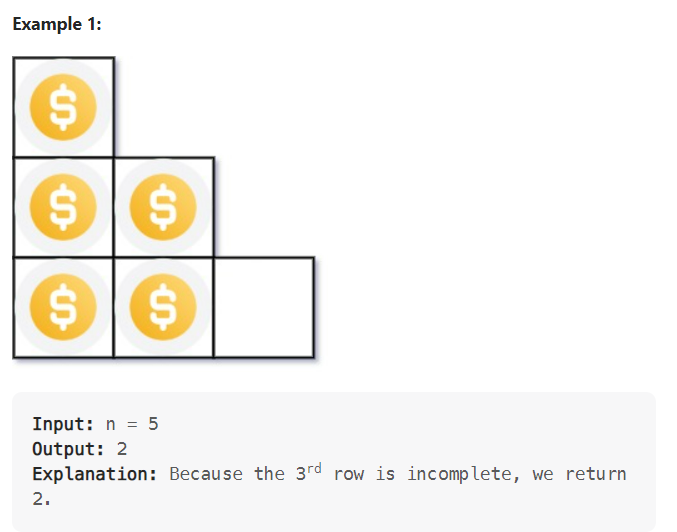
예시 1: n이 5임으로 5 = 1 + 2 + 2(incomplete) 즉 1행과 2행이 완전히 채워져 있으므로 2를 반환한다.

예시 2: n이 8임으로 8 = 1 + 2 + 3 + 2(incomplete) 즉 1행과 2행과 3행이 완전히 채워져 있으므로 3을 반환한다.
풀이:
1. 단순한 반복문을 통한 풀이
class Solution {
// 시간 복잡도 O(n) 공간 복잡도 O(1)
public int arrangeCoins(int n) {
int i=1;
while(n>0){
n-=i++;
}
if(n==0) return i-1;
return i;
}
}2. 이진 탐색을 활용한 풀이
class Solution {
// 시간 복잡도 O(log n) 공간 복잡도 O(1)
public int arrangeCoins3(int n) {
long start=0,end=n; // 0~n의 범위에서 탐색
long k,curr;
while(start<=end){
// start + (start-end)/2 도 가능?
k = (start+end)/2;
curr = k*(k+1)/2;
// k값을 찾은 상태
if(curr==n) return (int)k;
// 찾는 k값이 해당 값보다 순서상 왼쪽에 있는(작은) 상태
if(n<curr){
end = k-1;
}
// 찾는 k값이 해당 값보다 순서상 오른쪽에 있는(큰) 상태
else{
start = k+1;
}
}
// 반복에서 벗어 났다는 것은 최하층이 불완전 한 채로 존재 한다는 것
// 따라서 start 만큼 층이 존재하나 전부 채워진 층은 end 층 까지
return (int)end;
}
}3. 가우스 합 공식을 활용한 방법 (LeetCode 공식 풀이법)
가우스 합 공식이란? 1~k 까지의 합계를 (항의 수)*(첫 항+마지막 항)/2 를 통해 구할 수 있는 공식
즉 k*(k+1)/2 <= n 의 관계식을 통해 k = f(n) 의 식으로 유도하여 푸는 것

class Solution {
// 시간 복잡도 O(1) 공간 복잡도 O(1)
public int arrangeCoins4(int n) {
return (int)(Math.sqrt(2 * (long)n + 0.25) - 0.5);
}
}링크: https://leetcode.com/problems/arranging-coins/description/
'PS > Easy' 카테고리의 다른 글
| 448. Find All Numbers Disappeared in an Array (해석 + 풀이) (0) | 2023.01.04 |
|---|---|
| 520. Detect Capital (해석 + 풀이) (1) | 2023.01.03 |
| 434. Number of Segments in a String (해석+풀이) (0) | 2023.01.01 |
| 414. Third Maximum Number (해석) (0) | 2022.12.30 |
| 412. Fizz Buzz (해석) (0) | 2022.12.29 |