<문제 설명>
<풀기 전 생각>
최단거리를 어떻게 구하느냐가 가장 큰 고민이었다.
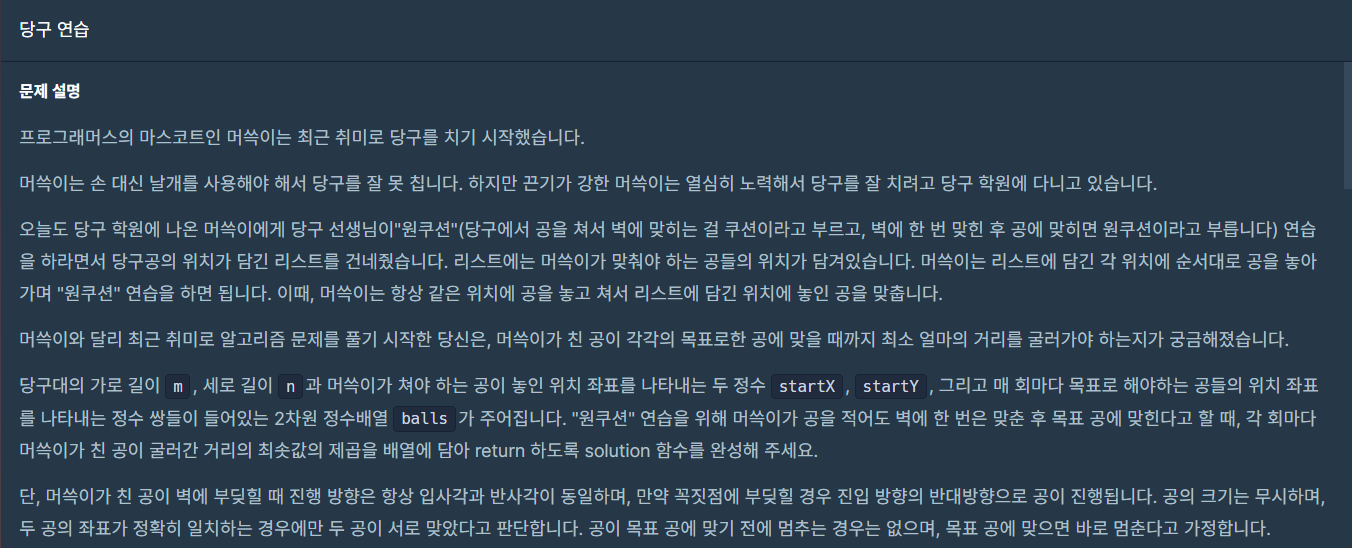
해당 문제에 대해 고민하고 알아보니 일단 공이 한 번 튕겨서 맞기 위해서는 입사각과 반사각이 같아야 하기
때문에 반사각의 성질을 활용하여 생각해보면 맞추어야 할 공을 반사면에 대칭 시킨다면
시작하는 공의 위치에서 대칭이동 된 맞추어야 할 공의 거리가 원쿠션으로 공을 맞출 경우의 거리임을 알 수가 있다.
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=yh6613&logNo=220147018035 (자료 및 학습한 자료 링크)
이제 원쿠션으로 공을 맞추었을때 의 길이를 구하는 방식은 해결 되었고 따라서
반사면이 총 4개가 존재하므로 각각의 경우를 체크하여 가장 짧은 최단거리를 구하면 된다
<중간 실패>
그렇게 코드를 짜고 돌려본 결과 29~36번 테스트에서 실패가 나왔고
원인을 살펴보니 두개의 공의 x좌표 혹은 y좌표가 같은 경우 반대쪽 벽면을 치고 원쿠션을 하는 경우를 체크하지 않아서 임을 파악했고 해당 경우를 체크하도록 코드를 수정하니 Pass 할 수 있었다.
<최종 코드>
import java.util.ArrayList;
import java.util.List;
class Solution {
// 시간 복잡도 O(4n) 이때 n은 balls 배열의 숫자 이다. 공간 복잡도 O(n)
public int[] solution(int m, int n, int startX, int startY, int[][] balls) {
List<Integer> answer = new ArrayList<Integer>();
for (int []ball:balls) {
int ans = Integer.MAX_VALUE;
double tmp = 0;
if(ball[0] == startX){
if (ball[1] > startY)
tmp = Math.pow(ball[1]+startY, 2);
else
tmp = Math.pow(2*n - ball[1]- startY, 2);
}
else if(ball[1] == startY){
if (ball[0] > startX)
tmp = Math.pow(ball[0]+startX, 2);
else
tmp = Math.pow(2*m - ball[0]- startX, 2);
}
if(tmp!=0)
ans = (int)tmp;
int[][] mirrorPoints = new int[4][2];
// y 축 대칭
mirrorPoints[0] = new int[]{-ball[0], ball[1]};
mirrorPoints[1] = new int[]{2 * m - ball[0], ball[1]};
// x 축 대칭
mirrorPoints[2] = new int[]{ball[0], -ball[1]};
mirrorPoints[3] = new int[]{ball[0], 2 * n - ball[1]};
for (int[] mirrorPoint : mirrorPoints) {
if(mirrorPoint[0]==startX||mirrorPoint[1]==startY)
continue;
tmp = Math.pow(mirrorPoint[0] - startX, 2) + Math.pow(mirrorPoint[1] - startY, 2);
if (ans >= tmp)
ans = (int) tmp;
}
answer.add(ans);
}
return answer.stream().mapToInt(i->i).toArray();
}
}<좀 더 생각해 봐야 하는 점>
개인적인 생각으로는 지금은 모든 벽면을 튕기는 경우를 일일이 체크하여 값을 비교하고 있는데
모든 경우를 체크하기 전에 논리적으로 어떤 벽을 튕기는 경우가 최단 거리임을 파악하고 OnePass 알고리즘으로 짤 수 있지 않을까 하는 생각이 든다.
메모: 수학적인 개념을 다시 복습할 필요성을 느낄 수 있던 문제였다
'PS > Level1' 카테고리의 다른 글
| 대충 만든 자판 (0) | 2023.02.26 |
|---|---|
| 둘만의 암호 (0) | 2023.02.19 |
| 자연수를 뒤집어 배열로 만들기 (0) | 2023.02.18 |
| 크레인 인형뽑기 게임 (0) | 2023.02.06 |
| 로또의 최고 순위와 최저 순위 (3) | 2023.02.04 |