
조건:
- n == gas.length == cost.length
- 1 <= n <= 105
- 0 <= gas[i], cost[i] <= 104
의역: n개의 가스 주유소가 원형으로 존재할 때 gas[i] 배열은 각각의 가스 주유소에서 주유할 수 있는 가스량을 나타내고 cost[i] 배열은 i번째 정류장에서 i+1의 가스 정류장으로 이동할 때 드는 가스의 양을 나타낸다. (만약 i+1이 인덱스 범위를 넘어 간다면 원형으로 이동 한다고 생각하고 0번 인덱스로 넘어간다)
시작하는 정류장의 위치를 마음대로 정할 수 있을 때 시계방향으로 ex 3 -> 4 -> 5- > 0 -> 1 -> 2 -> 3 한 바퀴를 도는 것이 가능 한 정류장의 위치를 반환하라 만약 존재하지 않을 경우 -1을 반환한다.
(만약 시계방향으로 한 바퀴를 도는 것이 가능 하다면 답은 고유성을 보장한다.)

의역: 인덱스 3번 정류장에서 시작 하여 연료 4를 채우고 0 + 4 = 4
4번 정류장으로 이동 후 연료 보급 4 - 1 + 5 = 8
0번 정류장으로 이동 후 연료 보급 8 - 2 + 1 = 7
1번 정류장으로 이동 후 연료 보급 7 - 3 + 2 = 6
2번 정류장으로 이동 후 연료 보급 6 - 4 + 3 = 5
3번 정류장으로 이동 5 - 5 = 0
3번 정류장에서 시작하여 시계방향으로 한 바퀴 도는 것이 가능하므로 3을 반환
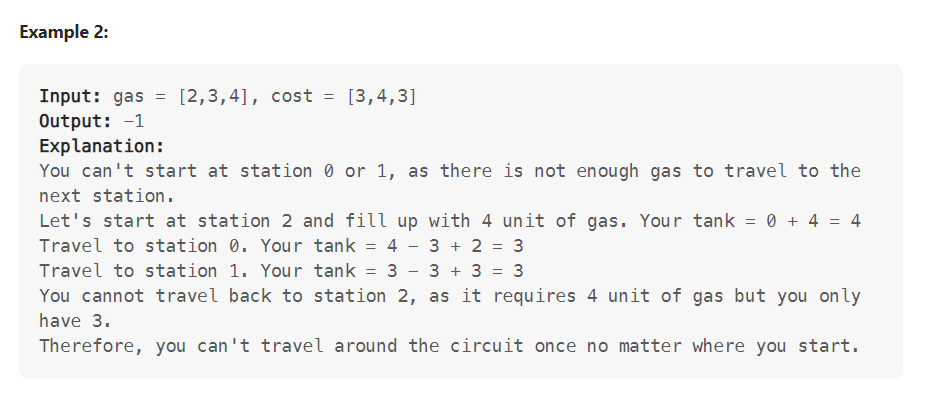
의역: 인덱스 0번과 1번에서 출발 할 경우 다음 정류장 으로 이동하는 것이 불가능 하기 때문에 2번 인덱스에서 시작한다
2번 정류장에서 연료 4를 채우고 0 + 4 = 4
0번 정류장으로 이동 후 연료 보급 4 - 3 + 2 = 3
1번 정류장으로 이동 후 연료 보급 3 - 3 + 3 = 3
2번 정류장으로 이동이 불가능 3 - 4 = -1
따라서 모든 경우의 수에서 시계방향으로 한 바퀴 도는 것이 불가능하므로 -1을 반환
풀이:
1. Vector와 Collections.sort() 함수 사용(만약 사용 x시 시간 초과) <브루트 포스>
단순히 출발지가 될 수 있는 인덱스를 Vector에 더하고 각각의 정류장에서 반복문을 통해 성공시 탈출 실패시 탈출x
import java.util.Collections;
import java.util.Comparator;
import java.util.Vector;
class Solution {
// 시간 복잡도 O(n^2) 공간 복잡도 O(n)
public int canCompleteCircuit(int[] gas, int[] cost) {
if(gas.length==1&&gas[0]>=cost[0]) return 0;
int remain = 0;
Vector<Integer> v = new Vector<Integer>();
// 시작점이 가능한 곳 만 Vector에 추가
//v.removeIf(n->(gas[n]-cost[n]==0)); >= 으로 바꾸고 해당 문장을 써도 됨
for(int i=0;i<gas.length;i++){
// if(gas[i]-cost[i]>=0)시 time out
if(gas[i]-cost[i]>0) {
v.add(i);
}
remain+=gas[i];
remain-=cost[i];
}
// 만약 시작점이 가능한 곳이 존재x 라면 종료
if(v.size()==0||remain<0) return -1;
remain = 0;
// 더 빠르게 한다면... 음 gas - cost의 값이 제일 작은 곳 혹은 제일 큰 곳 부터 시작?
// 1. 시작점 설정하기, 2. 다음 칸으로 이동 결과가 +-0이면 스킵하기?
// 모든 결과는 유일할 수 밖에 없는 세트를 제공한다고 함
// gas[i]-cost[i] 값을 기준으로 내림차순 정렬
Collections.sort(v, new Comparator<Integer>() {
public int compare(Integer p1, Integer p2) {
if(gas[p1]-cost[p1] > gas[p2]-cost[p2]) {
return -1; //맨 앞으로
}
else if(gas[p1]-cost[p1] == gas[p2]-cost[p2]) {
return 0;
}
else {
return 1; // 맨 뒤로
}
}
});
// gas[i] - cost[i]가 큰 곳 부터 차례대로 가능 불가능 여부 탐색
for(int i=0;i<v.size();i++){
for(int j=0;j<gas.length;j++){
if(remain<0) break;
int index = v.get(i)+j;
remain+=gas[index%gas.length];
remain-=cost[index%gas.length];
}
if(remain>=0)
return v.get(i);
else
remain = 0;
}
// 모든 경우 탐색 결과 실패시 -1 반환
return -1;
}
}
Collections.sort() 함수를 이용한 Vector 정렬 추천 글: https://hsdevelopment.tistory.com/474
2. 백트레킹 (논리적으로 무조건 실패하는 경우는 검사 하지 않고 스킵)

만약 0번 주유소에서 시작하고 3번 주유소에서 4번으로 가는 도중 연료가 다 떨어져 실패했다고 가정했을 때
현재 주유소에서 다음 주유소로 이동하는데 성공했다는 것은 (주유하는 연료 - 소비하는 연료)값이 +임을 의미하므로
0~3번 주유소까지 이동하는 동안 (주유하는 연료 - 소비하는 연료)+로 증가한 수치보다 정류소 3에서 - 되는 수치가 높다면 0번 말고 1번 2번에서 출발하여도 결과는 실패로 나올 것이다.
따라서 반복을 통해서 0번 주유소부터 출발하여 실패 시 실패한 정류소+1의 위치에서 다시 시작한다고 가정을 하면
시간 복잡도를 O(n^2)에서 O(n)로 줄이는 것이 가능하다.
class Solution {
// 시간 복잡도 O(n) 공간 복잡도 O(1)
public int canCompleteCircuit(int[] gas, int[] cost) {
int totalGas = 0;
int curGas = 0;
int ans = 0;
// 해당 반복을 통해 원형으로 돌 수 있는 시작 정류소가 존재할 경우는 검출 가능하나
// 가능한 정류소가 아애 존재 하지 않는 경우는 검출 불가능 따라서 totalGas변수 추가 사용
for(int i=0;i<gas.length;i++){
curGas +=(gas[i]-cost[i]);
if(curGas<0){
totalGas += curGas;
curGas = 0;
ans = i+1;
}
}
totalGas += curGas;
// 만약 전체 totalGas의 양이 -라면 가능한 정류소가 없다는 뜻
// why? 모든 정류장을 이동 할때 (얻는 가스 - 소비하는 가스) < 0 인 상황이므로
return totalGas<0?-1:ans;
}
}
'PS > Medium' 카테고리의 다른 글
| 133. Clone Graph (bfs,dfs) (0) | 2023.04.08 |
|---|---|
| 200. Number of Islands, 1254. Number of Closed Islands, 1020. Number of Enclaves (dfs, bfs) 문제 (0) | 2023.04.07 |
| 1833. Maximum Ice Cream Bars (0) | 2023.01.07 |
| 452. Minimum Number of Arrows to Burst Balloons (해석 + 풀이) (0) | 2023.01.06 |
| 55. Jump Game (해석) (0) | 2022.12.27 |